오일러 Transform

오일러 Transform에서
오일러 각을 이용해서 x축, y축, z 축으로 얼마 회전했는지를 쉽게 알 수 있다
주의할 점은,
행렬의 교환법칙은 성립하지 않기 때문에
x, y, z축의 회전행렬의 곱의 순서에 따라 결과는 달라진다는 점이다
Key Frame Animation
Key Frame Animation이란
아래의 그림처럼
특정 키 프레임의 간격 사이에서 발생하는 부분을 자연스럽게 채워 넣는 부분으로
lerp(linear interpolation)를 통해 이를 구현한다

또한, 좀더 자연스럽게 이를 구현하기 위해서
linear가 아닌 curve를 이용하기도 한다

오일러 각의 문제점
아래의 예시를 보면 알다시피
오일러 각 x, y, z 축을 interpolation을 하는 경우에 비틀리는 문제가 발생한다
반면, Quaternion을 이용하면 해당 문제가 발생하지 않는다

비틀려지는 문제를 확인하려면,
게임 상용엔진에서는 Quaternion으로 자체적으로 연산하기에 확인하기는 어렵다
블랜더에서는 수동으로 Euler, Quaternion을 선택할 수 있어서
아래와 같은 문제가 되는 상황을 직접 확인할 수 있다

이러한 문제가 발생하는 이유는
3차원의 축들은 매우 복합적이지만
오일러 각은 각각의 축들을 독립적으로 계산하다 보니 발생하는 문제이다
또한,
y축이 90도 혹은 -90도로 회전을 하면 x축과 z축이 겹쳐지는
짐벌락 현상으로 인해 발생하는 문제이다
짐벌락 현상 참고 영상:
https://youtu.be/vHr77Dre25Q?feature=shared
Quaternion(사원수)
- Quaternion은 복소수의 확장이다
i, j, k라는 허수를 추가해서 아래의 개념을 나타냈다
그리고 한 차원을 증가하기 위해서 w가 등장했다
qx, qy, qz의 imaginary 부분과 qw의 w 부분으로 구분을 하고
(qv, qw)라고 표현한다

- 복소수 공간에서는 아래의 규칙이 성립된다
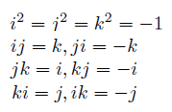
- 복소수의 곱은 아래와 같은 형태를 띤다
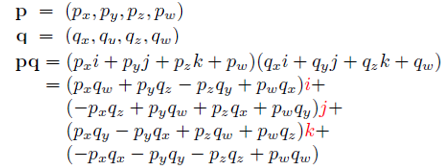
- Conjugate를 하면 아래와 같이 연산된다
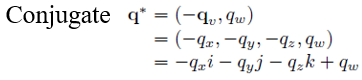
- 아래의 법칙이 성립한다

- 길이가 1인 unit quaternion은 아래와 같이 계산할 수 있다
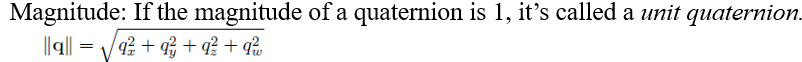
복소수의 2D Rotation
행렬을 통해 회전을 연산하는 오일러와는 달리
복소수 개념을 가지고
점의 좌표와 θ를 복소수화하면 아래와 같은 결과가 나온다

위를 보다시피
pq의 곱의 결과는 실수 부분이 x좌표, 허수 부분이 y좌표가 된다는 것을 알 수 있다
복소수의 3D Rotation

2D와 비슷하게
3D에서도
1) 점의 좌표를 Quaternion으로 변환하고
2) u(회전축)와 θ(회전 각도)를 이용해, q라는 Quaternion을 나타내고
3) qpq*를 계산한 값의 허수 부분을 통해 회전 벡터 결과 값을 도출해 낼 수 있다
Quaternion 보간

참고로 위 그림의 구는 실제 4차원의 구가 아닌
이해를 돕기 위한 가상의 구를 그려놓은 것이다
Quaternion에서의 보간은 위의 하이라이트 된 공식을 통해 연산한다
이러한 보간은 slerp라고 부르고
최단 거리로 보간을 진행하기 때문에 오일러처럼 비틀리는 문제가 발생하지 않는다
게임엔진에서의 Quaternion 보간
Quaternion은 4차원으로 직관적이지 않고 가독성이 좋지 않다
따라서
엔진은 개발자에게 오일러 interpolation처럼 값을 받지만
실제로 연산은 Quaternion으로 변환해서 slerp를 진행한다
또한,

위의 그림에 나오는 공식을 이용해서
Quaternion과 Rotation Matrix의 변환이 가능하다
따라서,
셰이더에서 뿐 아니라
실제 컴퓨터 그래픽스 연산에서는 Rotation Matrix를 이용한 곱연산이 기본이기에
slerp를 해서 중간값을 얻더라도
실제 연산을 할 때는 Quaternion을 Rotation Matrix로 바꿔서 연산처리를 한다
'게임 그래픽스 > [전북대] OpenGL' 카테고리의 다른 글
| [OpenGL Note] Shadow Map (0) | 2024.11.25 |
|---|---|
| [OpenGL Note] Normal Map (0) | 2024.11.25 |
| [OpenGL Note] Output Merger - Alpha Blending (0) | 2024.04.20 |
| [OpenGL Note] Output Merger - Z buffering (0) | 2024.04.20 |
| [OpenGL Note] Lighting - Ambient, Emmisive (0) | 2024.04.19 |
