[코테 합격자 되기] 09장 트리

# 트리의 개념

트리는 노드와 간선으로 이루어진 계층적 자료구조로

부모-자식 관계가 존재한다

트리는 순환이 허용되지 않는다

코테에서는 이진트리(자식 노드가 최대 2개인 트리)가 핵심이다

 

노드는 루트노드, 자식노드, 형제노드, 리프노드 등의 종류로 구분된다

차수는 현재 노드를 기준으로 바로 아래에 있는 자식노드의 개수를 의미한다

레벨은 0부터 시작하며, 하나의 줄을 의미한다

높이는 현재 트리에서 최대 레벨을 의미한다

 

---

 

# 이진트리의 표현 (배열)

이진트리를 배열로 표현할 수 있다

루트노드 인덱스를 1로 선정하고

왼쪽 자식노드는 부모노드 인덱스 * 2

오른쪽 자식노드는 부모노드 인덱스 * 2 + 1와 같은 구성을 띤다

 

이처럼 위의 인덱스 공식만을 활용하기에 구현 난이도는 낮다

하지만, 실제 사용되지 않는 빈 공간이 많다는 단점이 있다

 

# 이진트리의 표현 (인접리스트)

이진트리를 인접리스트로 표현할 수 있다

각 리스트의 인덱스는 부모노드로

자식노드는 부모노드에 해당되는 인덱스에 추가하는 방식이다

 

배열보다 공간 효율이 좋다

하지만, 자식 노드를 찾기 위해 순차탐색을 해야 하기에 오래 걸릴 수 있다

단, 코테에서 사용되는 트리는 거의 자식이 2개인 2진 트리이기에 오래 걸리지 않는다 

 

---

 

# 이진트리의 순회

트리의 노드를 모두 방문하는 것을 순회라고 한다

순회 방법에는 현재노드를 언제 방문하는지에 따라서 

전위순회, 중위순회, 후위순회로 분류된다

 

- 전위순회

루트노드부터 시작해서

부모노드 > 왼쪽 자식노드 > 오른쪽 자식노드 순으로 방문한다

 

이러한 방식은
루트노드부터 트리 노드를 순차적으로 방문하고
부모부터 차례대로 복사되는 특징이 있다

 

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Algorithm_with_DataStructure/preorder_tree_array.cpp

 

- 중위순회

루트노드 부터 시작해서

왼쪽 자식 노드 > 부모노드 > 오른쪽 자식노드 순으로 방문한다

 

이러한 방식은
이진탐색트리의 원소를 정렬된 상태대로 순회 가능하다는 특징이 있다
따라서, 왼쪽은 부모보다 먼저 호출되고 오른쪽은 부모보다 나중에 호출된다 

 

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Algorithm_with_DataStructure/inorder_tree_array.cpp

 

- 후위순회

 

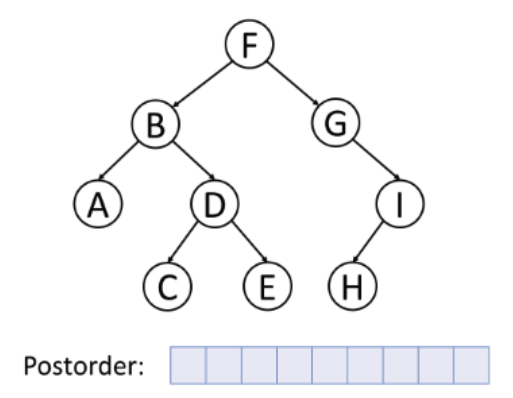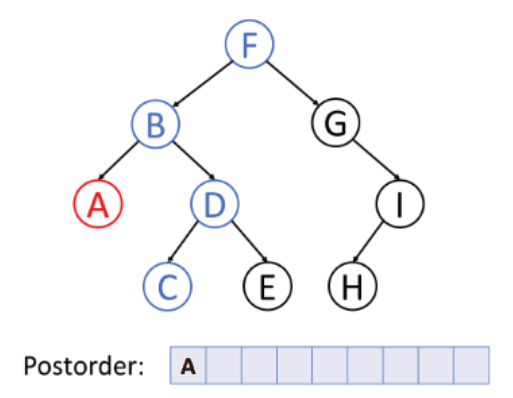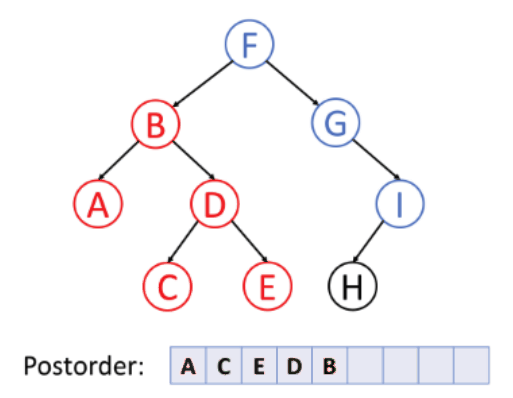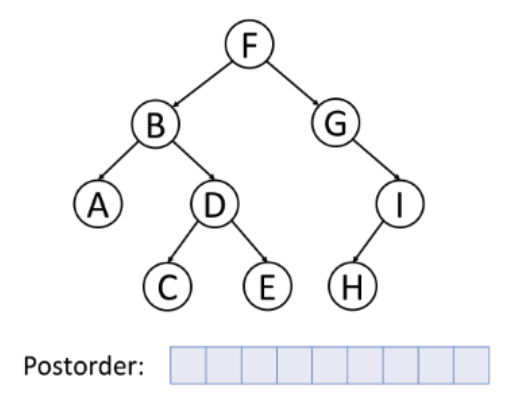
루트노드부터 시작해서
왼쪽 자식노드 > 오른쪽 자식노드 > 부모노드 순으로 방문한다

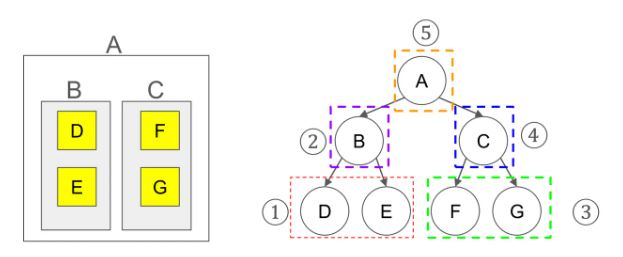
이러한 방식은
루트노드를 기준으로 각각 제일 깊숙이 들어있는 원소부터 방문하고
폴더 삭제를 하는 경우에 이와 같은 방식이 사용된다

 

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Algorithm_with_DataStructure/postorder_tree_array.cpp

 

---

 

# 이진탐색트리

- 개념

탐색을 효율적으로 하기 위해 만든 이진트리이다

왼쪽 자식노드는 부모노드보다 작은 값이고

오른쪽 자식노드는 부모노드보다 큰 값이 온다

 

- 특징

탐색) 최대탐색 횟수는 트리의 높이와 같다 (최악: O(N), 균형 유지: O(logN))

삽입, 정렬) 삽입과 동시에 정렬을 한다 (최악: O(N), 균형 유지: O(logN))

map, set의 내부는 균형이진탐색트리로 key값 기준으로 정렬한다 

 

- 삽입

 

- 탐색

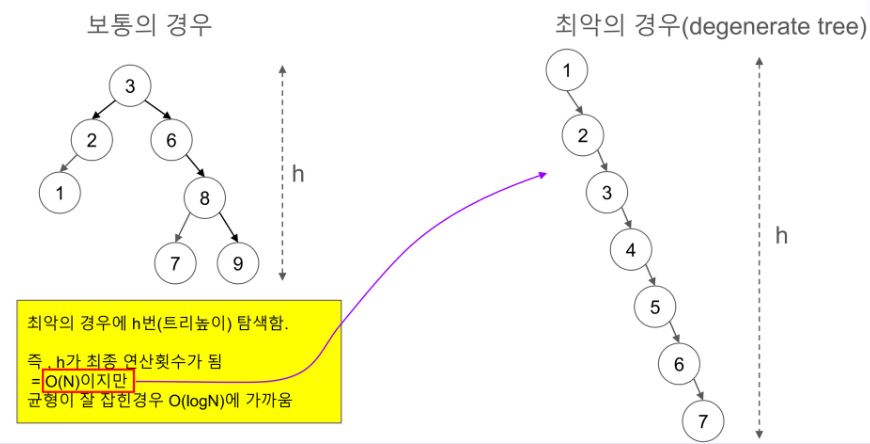
균형이 잘 잡힌 경우에는 O(logN)

최악의 경우에는 h(높이) 번 탐색을 해야 하기에 O(N)이 걸린다