[코테 합격자 되기] 10장 집합

#상호배타적 집합

위의 왼쪽 그림처럼

교집합이 없는 집합관계를 상호배타적 집합이라고 한다

 

#집합을 표현하는 방식

집합을 표현할 때,

집합에서 가장 작은 원소를 대표 원소로 설정하고

현재 노드의 부모노드를 저장하는 array나 unordered_map을 통해 테이블을 만들면 된다

 

테이블에는 본인의 부모노드를 작성한다

현재노드와 부모노드가 동일한 경우는 대표원소이다

부모노드가 -1은 미존재 원소를 의미한다

 

---

 

#집합의 연산 - find

특정 노드의 루트노드를 확인하는 연산이다

특정 노드로부터, 루트노드가 나올 때까지 거슬러 올라가면 된다

 

그런데,

find에서 내부 처리 방식은 2가지 종류가 있다

1) 반환하고 거슬러올라가 방문한 노드의 부모노드도 다 바꾸는 방식

2) 그냥 반환하고 끝내는 방식

 

예를 들어,

위의 그림 집합 A에서 find(7)을 하게되면

1번 방식을 활용하면,

거슬러 올라가며 방문한 2 6 7의 부모노드를 모두 1로 바꾸고 1을 반환하는 것이다

2번 방식을 활용하면,

거슬러 올라서 그냥 루트노드만 반환하는 것이다 

 

# find의 문제

위의 그림처럼

집합의 깊이가 깊은 경우에는, 루트노드를 찾기 위해 O(N)이 걸릴 수도 있다

 

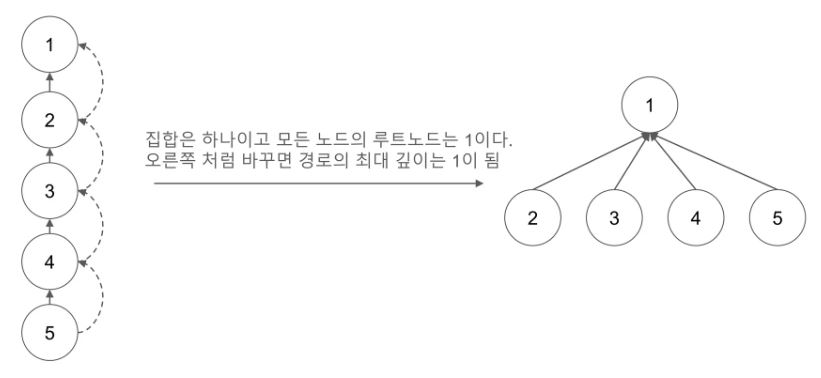
따라서, 이를 해결하기 위해 경로압축알고리즘을 이용하면 된다

앞서 언급되었던 find의 내부 방식 중

2번 방식은 경로압축을 적용하지 않은 예시였다

1번 방식은 경로압축을 적용한 예시였다

 

# 경로압축

경로 압축 방식

경로 압축 결과

경로압축을 통해 트리의 깊이를 최소화할 수 있다

경로 압축을 하지 않으면, find연산이 최악의 경우는 O(N)이지만

경로압축을 하면, O(1)이 걸린다

단, 거쳐간 노드들만 경로압축이 됨 - 예시 사진

 

---

 

# 집합의 연산 - union

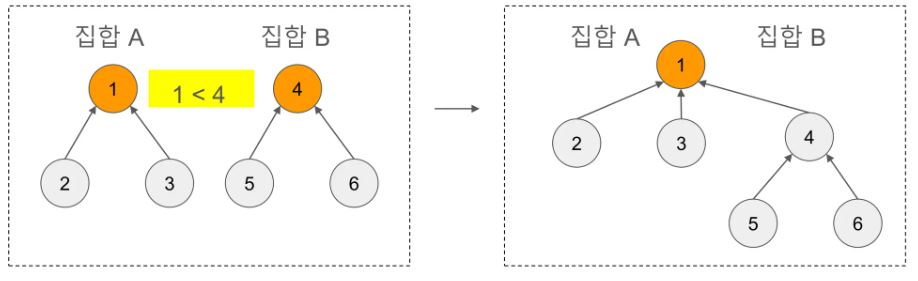
union은 두 개의 집합을 하나의 집합으로 합치는 연산으로

한쪽 루트노드를 다른 쪽 루트노드에 연결하는 것이다

어떤 루트노드가 연결될지는 다양한 방법이 있다

대표적으로는 큰 쪽 루트노드의 부모노드를 작은 쪽 부모노드로 변경하는 방식이 있다

 

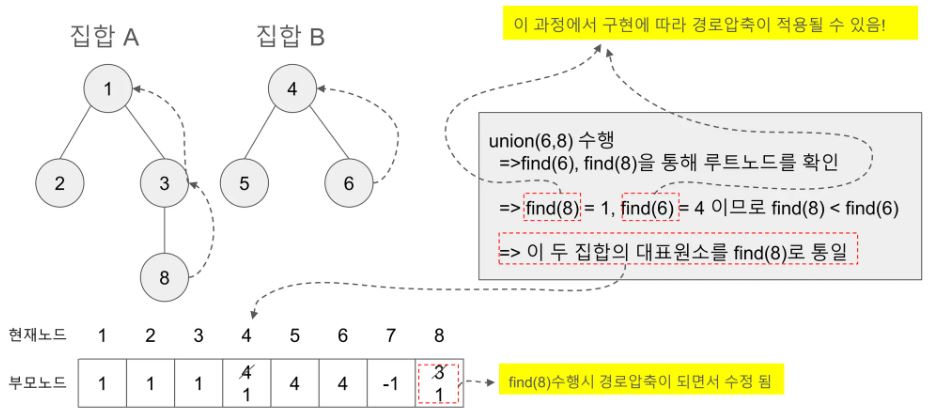
union 연산 내부 과정은

find를 이용하고 상황에 따라 경로압축알고리즘은 적용하면 된다

 

# union의 문제

union으로 합쳤을 때 트리의 깊이가 깊어지면 find의 시간이 오래 걸린다

따라서, 트리의 깊이를 최소화하며 합치기 위한 방법으로

랭크기반 알고리즘으로 개선한다

 

# 랭크기반 알고리즘

위의 그림처럼 현재 노드 기준 트리 최대 높이를 랭크라고 한다

 

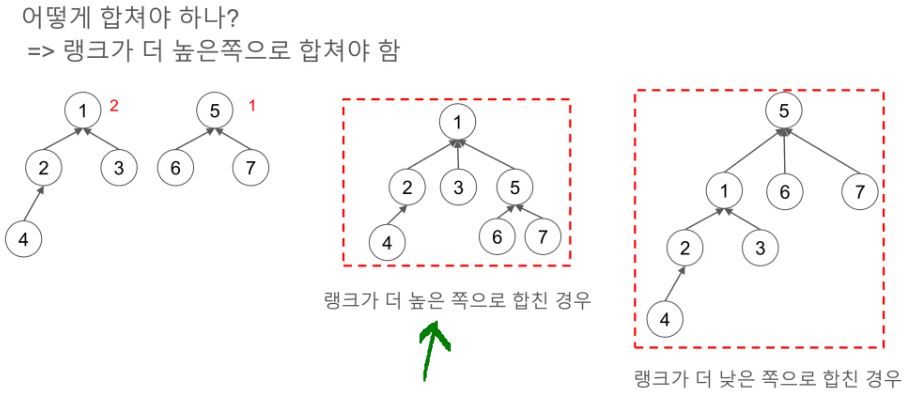
위의 그림처럼

각각 루트 노드의 랭크를 비교해서

랭크가 높은 루트노드 쪽으로 합치는 방식이다

 

---

 

# 집합의 구현

최대 개수가 작은 경우는 array를 사용해서 구현하면 되고

최대 개수가 큰 경우는 unordered_map을 사용해서 구현하면 된다

또한,

집합은 정렬할 필요가 없으니, map을 사용해서는 안되며

정렬 때문에 TLE 발생할 수 도 있다

 

- array 활용 (경로압축기반 X)

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Algorithm_with_DataStructure/unionfind_not_optimization.cpp

 

- array 활용 (경로압축기반 O)

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Algorithm_with_DataStructure/unionfind.cpp

 

- unordered_map 활용 (경로압축기반 O)

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Algorithm_with_DataStructure/unionfind_with_unordered_map.cpp

 

 

# 집합을 언제 사용?

- 이미지 세그멘테이션

각 이미지를 각 객체 혹은 부분으로 분할해서

다른 색을 칠할 때 사용된다

 

- 네트워크 연결성 확인

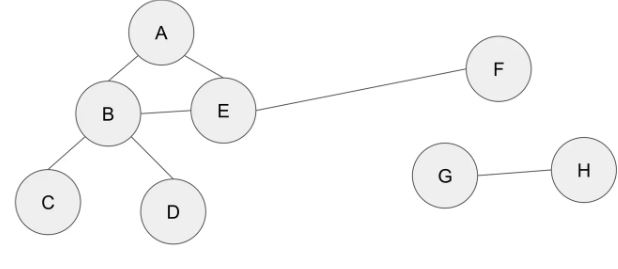
대규모 네트워크에서 두 컴퓨터가 서로 연결되어 있는지 확인할 때 사용된다

 

- 알고리즘 문제 (네트워크 연결성 확인)

주어진 노드와 연결된 간선으로 이루어진 네트워크에서

두 노드가 서로 연결되어 있는지 확인하는 문제이다

노드의 개수, 간선 목록, 그리고 쿼리 목록이 주어진다

 

예시 코드:

https://github.com/dremdeveloper/codingtest_cpp/blob/main/Example/network_connectivity_union_find.cpp