힙정렬

힙정렬은 힙구조의 heapify를 사용하는 것이 핵심이다
우선순위 큐에서 최대값 혹은 최소값을 pop 하면서 이를 활용하면
쉽게 사용가능하다
힙정렬 사용예시
void HeapSort(vector<int>& v)
{
priority_queue<int, vector<int>, greater<int>> pq;
// O(NlogN)
for (int num : v)
pq.push(num);
v.clear();
// O(NlogN)
while (pq.empty() == false)
{
v.push_back(pq.top());
pq.pop();
}
}
병합정렬

병합정렬은 분할정복이 핵심이다
분할정복 아이디어는 병합정렬뿐아니라 다양하게 활용된다 ex. 멀티스레드
병합정렬의 시간복잡도는
쪼개는데 logN이 필요하다
그리고 둘을 하나로 합치는데는 N이 필요하다
그런데 합치는 과정을 logN번 반복하니 NlogN이 필요하다
최종적으로는 logN(쪼개기) + NlogN(합치기) = O(NlogN)이 최종 시간복잡도이다
공간복잡도는 임시공간을 계속 만들어야 하다 보니 O(N)이다
병합정렬 예시

병합정렬 구현
void MergeResult(vector<int>& v, int left, int mid, int right)
{
// [2][3][7][4][8][9]
// [l] [m] [r]
int leftIdx = left;
int rightIdx = mid + 1;
vector<int> temp;
while (leftIdx <= mid && rightIdx <= right)
{
if (v[leftIdx] <= v[rightIdx])
{
temp.push_back(v[leftIdx]);
leftIdx++;
}
else
{
temp.push_back(v[rightIdx]);
rightIdx++;
}
}
// 왼쪽이 먼저 끝났으면, 오른쪽 나머지 데이터 복사
if (leftIdx > mid)
{
while (rightIdx <= right)
{
temp.push_back(v[rightIdx]);
rightIdx++;
}
}
// 오른쪽이 먼저 끝났으면, 왼쪽 나머지 데이터 복사
else
{
while (leftIdx <= mid)
{
temp.push_back(v[leftIdx]);
leftIdx++;
}
}
for (int i = 0; i < temp.size(); i++)
v[left + i] = temp[i];
}
void MergeSort(vector<int>& v, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) / 2;
MergeSort(v, left, mid);// 쪼개기
MergeSort(v, mid + 1, right);// 쪼개기
MergeResult(v, left, mid, right);// 합치기
}
퀵정렬

퀵정렬의 핵심은 pivot을 기준으로 low와 high를 통해 탐색하며 스왑 하는 것이다
퀵정렬의 방법은 아래와 같다
pivot을 정하고
low는 pivot보다 큰 값을 발견하고
high는 pivot보다 작은 값을 발견한 경우에 서로 swap을 진행한다
그리고 low와 high가 교차되면 종료한다
그리고 종료된 high와 pivot을 swap한다
이런 과정을 진행하면 pivot을 기준으로
왼쪽에는 작은 값들, 오른쪽에는 큰 값들이 분포하게 된다
그리고 좌/우를 새로운 pivot을 기준으로 또 각각 재귀적으로 위 작업을 진행하면 된다
시간복잡도는 low와 high가 각각 최대 이동을 N번한다
재귀적으로 호출되는 횟수의 경우는
처음 선정된 pivot이 중간 값에 가까울수록 평균 logN이 소모되고
처음 선정된 pivot이 중간 값에서 멀수록 최악 N이 소모된다
따라서, 최종적으로는 최악은 N^2, 평균은 NlogN이 발생한다
병합정렬과 비교하면, 시간복잡도는 동일하지만
사실상 조금 더 빠르고 공간복잡도도 O(logN)으로 훨씬 적다
퀵정렬 예시
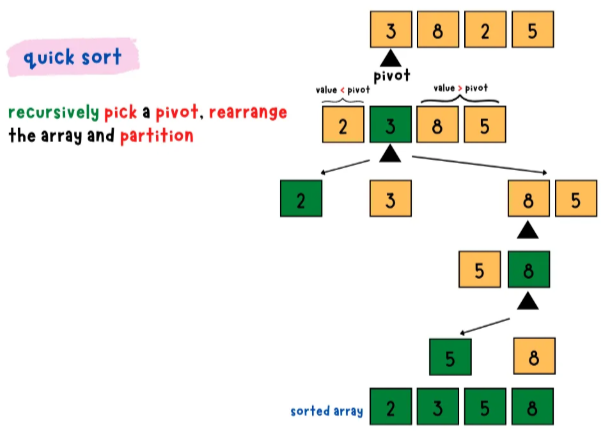
퀵정렬 구현
int Partition(vector<int>& v, int left, int right)
{
int pivot = v[left];
int low = left + 1;
int high = right;
// O(N)
while (low <= high)
{
while (low <= right && pivot >= v[low])
low++;
while (high >= left + 1 && pivot <= v[high])
high--;
if (low < high)
swap(v[low], v[high]);
}
// pivot과 high의 교체
swap(v[left], v[high]);
return high;
}
// O(N^2) < 최악
// O(NlogN) < 평균
void QuickSort(vector<int>& v, int left, int right)
{
if (left > right)
return;
int pivot = Partition(v, left, right);
QuickSort(v, left, pivot - 1);
QuickSort(v, pivot + 1, right);
}
정렬 시/공간 복잡도
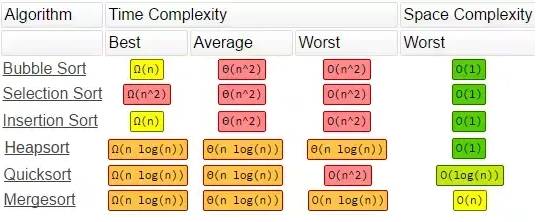
힙, 머지, 퀵 모두 시간복잡도 평균은 O(NlogN)이다
공간복잡도는 힙은 O(1), 머지는 O(N), 퀵은 O(logN)이다
'자료구조 & 알고리즘 > [루키스] C++ 자료구조 & 알고리즘' 카테고리의 다른 글
| [C++ 자/알 Note] Disjoint Set (0) | 2025.01.23 |
|---|---|
| [C++ 자/알 Note] 해시테이블 (1) | 2025.01.19 |
| [C++ 자/알 Note] 정렬 - 버블, 선택, 삽입 (0) | 2025.01.19 |
| [C++ 자/알 Note] 레드블랙트리 - 삭제 (0) | 2025.01.19 |
| [C++ 자/알 Note] 레드블랙트리 - 개념 및 삽입 (0) | 2025.01.19 |
