동적 계획법 (Dynamic Programming, DP)
복잡한 문제를 작은 하위 문제들로 나누어 해결하고,
그 결과를 저장해 두었다가 재활용함으로써
중복 계산을 피하고 효율적으로 문제를 해결하는 알고리즘 설계 기법이다
동적 계획법 조건
아래의 두 가지 조건을 모두 만족해야 한다
1) 최적 부분 구조 (Optimal Substructure):
큰 문제의 최적 해가 작은 하위 문제들의 최적 해를 포함하고 있는 구조
2) 중복되는 하위 문제 (Overlapping Subproblems):
동일한 하위 문제가 여러 번 반복적으로 나타나는 경우
동적 계획법 방식
1) Top-Down (재귀 + 메모이제이션):
큰 문제에서 시작하여 재귀적으로 하위 문제를 해결하면서 결과를 저장하고
메모이제이션을 활용한다
2) Bottom-Up (반복):
작은 하위 문제부터 차례대로 해결하면서 결과를 저장하고,
이를 이용하여 큰 문제의 해를 구함
메모이제이션 (Memoization)
DP를 구현하는 전략 중 한 가지이다
함수 호출 결과를 저장해 두고, 동일한 입력으로 함수가 다시 호출될 때
저장된 결과를 반환하여 중복 계산을 피하는 기법이다
메모이제이션은 DP의 중요한 요소 중 하나이지만, 모든 DP 구현에 필수적이지 않다
Bottom-Up 방식의 DP에서는 별도의 저장 공간에 하위 문제의 결과를 저장하여
메모이제이션 없이도 DP를 구현할 수 있다
Top-Down 방식의 DP에서는 메모이제이션을 필수적으로 사용하며,
재귀 호출을 통해 문제를 해결하는 과정에서 중복 계산을 줄이기 위해 계산 결과를 저장한다
예시 1 - 피보나치 수열

- DP를 사용하지 않는 재귀 (Naive Recursive Approach) 방식
int fib(int n)
{
if (n <= 1)
{
return n;
}
return fib(n - 1) + fib(n - 2);
}
이 코드는 중복되는 하위 문제 (ex. fib(3)이 여러 번 호출됨)가 많아 효율성이 매우 떨어진다
- Top-Down DP (Memoization) 방식
std::unordered_map<int, int> memo;
int fib_memo(int n)
{
if (memo.count(n))
{
return memo[n];
}
int result;
if (n <= 1)
{
result = n;
}
else
{
result = fib_memo(n - 1) + fib_memo(n - 2);
}
memo[n] = result;
return result;
}
memoization을 사용하여 이미 계산된 결과를 저장하고,
동일한 n 값으로 함수가 호출되면 저장된 결과를 반환해 중복 계산을 방지한다
- Bottom-Up DP (Tabulation) 방식
int fib_tabulation(int n)
{
if (n <= 1)
{
return n;
}
std::vector<int> dp(n + 1);
dp[1] = 1;
for (int i = 2; i <= n; ++i)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
작은 값부터 계산하여 결과를 테이블 (dp 배열)에 저장하고, 이를 이용하여 최종 결과를 도출한다
예시 2 - 이항계수
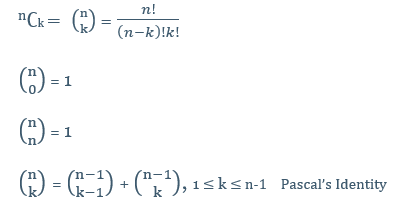

- DP를 사용하지 않는 재귀 (Naive Recursive Approach) 방식
int binomialCoeff_recursive(int n, int k)
{
if (k == 0 || k == n)
{
return 1;
}
return binomialCoeff_recursive(n - 1, k - 1) + binomialCoeff_recursive(n - 1, k);
}
- Top-Down DP (Memoization) 방식
std::unordered_map<std::string, int> memo;
int binomialCoeff_memo(int n, int k)
{
std::string key = std::to_string(n) + "," + std::to_string(k);
if (memo.count(key))
{
return memo[key];
}
if (k == 0 || k == n)
{
return 1;
}
int result = binomialCoeff_memo(n - 1, k - 1) + binomialCoeff_memo(n - 1, k);
memo[key] = result;
return result;
}
- Bottom-Up DP (Tabulation) 방식
int binomialCoeff_tabulation(int n, int k)
{
std::vector<std::vector<int>> dp(n + 1, std::vector<int>(k + 1, 0));
for (int i = 0; i <= n; ++i)
{
for (int j = 0; j <= std::min(i, k); ++j)
{
if (j == 0 || j == i)
{
dp[i][j] = 1;
}
else
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
}
return dp[n][k];
}'자료구조 & 알고리즘 > [루키스] C++ 자료구조 & 알고리즘' 카테고리의 다른 글
| [C++ 자/알 Note] TRIANGLE PATH 문제 (0) | 2025.01.27 |
|---|---|
| [C++ 자/알 Note] LIS (Longest Increasing Subsequence) 문제 (0) | 2025.01.26 |
| [C++ 자/알 Note] Prim 알고리즘 적용 (미로 생성) (0) | 2025.01.24 |
| [C++ 자/알 Note] Prim 알고리즘 (0) | 2025.01.24 |
| [C++ 자/알 Note] Kruskal 알고리즘 적용 (미로 생성) (0) | 2025.01.24 |
