벡터의 외적 유니티
벡터의 외적은 유니티에서 Vector3.Cross를 이용해 쉽게 구할 수 있다
법선벡터


면(두 벡터)의 수직인 벡터를 노멀라이즈 한 것을 법선벡터라고 한다
셰이더에서는 빛이 들어오는 방향과 비치는 부분 등을 계산하는데 활용되고
카메라에서는 보이는 부분인지 안 보이는 부분인지 컬링 하는데 활용된다
벡터의 외적 예시 1

위는 Vec1과 Vec2를 외적 한 벡터를 노란 공(cVec)을 통해 출력하는 예시이며
아래와 같이 구현 가능하다
void Update()
{
CrossVector();
Vector3 dir = cVec - Vec3.position;
if (dir.magnitude >= 0.1f)
Vec3.position += dir.normalized * Time.deltaTime;
}
void CrossVector()
{
cVec = Vector3.Cross(Vec1.position, Vec2.position);
//cVec = Vector3.Cross(Vec2.position, Vec1.position); //교환번칙 성립하지 않는다
Debug.Log(nameof(cVec) + ": " + cVec);
Debug.Log(nameof(Util.MyCross) + ": " + Util.MyCross(Vec1.position, Vec2.position));
System.Text.StringBuilder sb = new System.Text.StringBuilder();
{
sb.Append("Vec1: " + Vec1.position);
sb.Append("\n");
sb.Append("Vec2: " + Vec2.position);
sb.Append("\n");
sb.Append("cVec: " + cVec);
textMesh.text = sb.ToString();
}
}
벡터의 외적 예시 2

위는 목표 벡터를 향해 상하좌우 각도를 조절하는 모습이다
아래와 같이 구현 가능하다
void Update()
{
// 두 벡터의 방향 벡터
Vector3 dir = Player.position - Target.position;
// 외적
Vector3 cross = Vector3.Cross(Player.forward, dir);
// 좌우
float dotUP = Vector3.Dot(cross.normalized, Vector3.up);
// 상하
float dotRight = Vector3.Dot(crossFor.normalized, Vector3.right);
Debug.Log("cross: " + cross);
Debug.Log("dot: " + dotUP);
Debug.Log("dotFor: " + dotRight);
Util.DrawLine(LineDir, dir, Color.yellow, 50f);
//Util.DrawFowardLine(LineDir, crossFor, Color.yellow, 5f);
if (Input.GetKey(KeyCode.Space))
{
float angleY = dotUP > 0 ? -rotateSpeed : rotateSpeed;
float y = (angleY * Time.deltaTime) + Player.rotation.eulerAngles.y;
float angleX = dotRight > 0 ? -rotateSpeed : rotateSpeed;
float x = (angleX * Time.deltaTime) + Player.rotation.eulerAngles.x;
Player.rotation = Quaternion.Euler(x, y, 0);
}
System.Text.StringBuilder sb = new System.Text.StringBuilder();
{
sb.Append("cross: " + cross);
sb.Append("\n");
sb.Append("dot: " + dotUP);
sb.Append("\n");
sb.Append("dotFor: " + dotRight);
textMesh.text = sb.ToString();
}
}
Player.forward랑 dir을 외적 하는데
이 외적 한 값이 수평이 되면 0이 된다
두 벡터를 외적한 벡터와 Up벡터를 내적 해서 나오는 값이 음수, 양수, 0이냐 에따라 좌우 판단을 하고
두 벡터를 외적한 벡터와 Right벡터를 내적해서 나오는 값이 음수, 양수, 0이냐 에따라 상하 판단을 할 수 있다
벡터의 외적 예시 3

직사각형은 arcTan를 통해 각도를 알아내서 바로 적용한 것이고
원은 외적을 통해 수평이 될 때까지 각도를 조절하도록 작성한 것이다
아래와 같이 구현 가능하다
void Update()
{
if (target != null)
{
Vector3 dirVec = (target.position - transform.position);
float length = dirVec.magnitude;
if (length <= 0.01f)
{
index++;
index = (index >= Points.Length) ? 0 : index;
target = Points[index];
}
transform.position += transform.up * moveSpeed * Time.deltaTime;
Vector3 cross = Vector3.Cross(transform.up, dirVec);
float dotForward = Vector3.Dot(cross, Vector3.forward);
float angleZ = dotForward > 0 ? rotateSpeed : -rotateSpeed;
float z = (angleZ * Time.deltaTime) + transform.rotation.eulerAngles.z;
transform.rotation = Quaternion.Euler(0, 0, z);
}
// tanget를 통해 알아낸 직사각형의 코드
// float rot = Mathf.Atan(dirVec.y / dirVec.x);
// float degree = rot * Mathf.Rad2Deg;
// if (dirVec.x < 0)
// degree = 180 + degree;
// transform.rotation = Quaternion.Euler(0, 0, degree);
}
벡터의 외적 예시 4
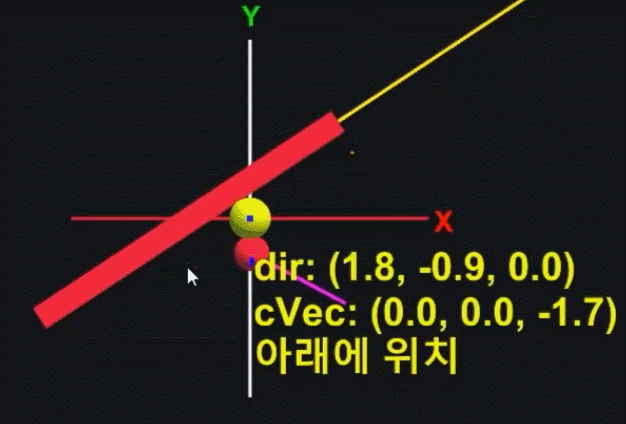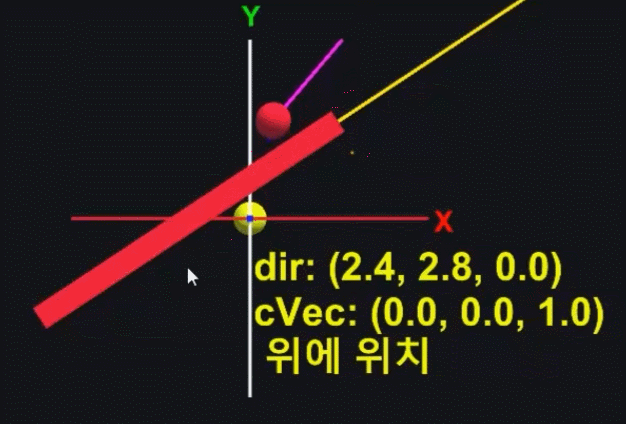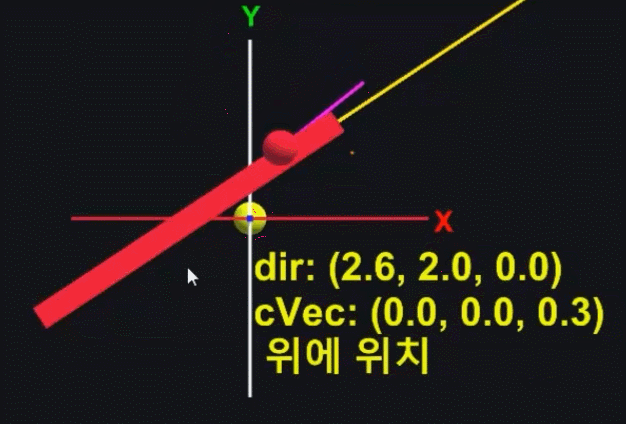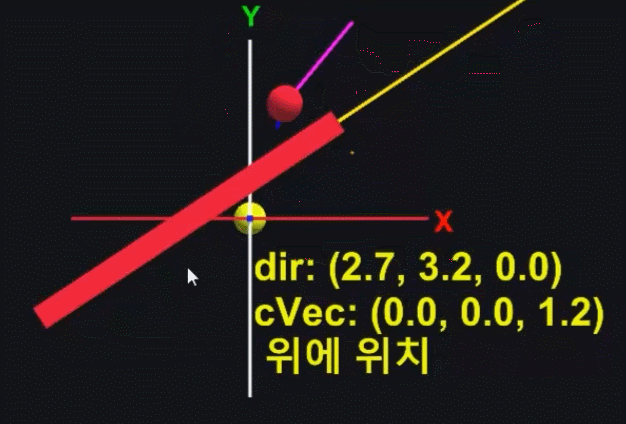
회전된 RotateVecTF를 기준으로 Vec(빨간 공)의 위아래 방향을 알아내는 예시이다
노란 선은 RotateVecTF의 Right를 의미하고
마젠타 선이 Vec(빨간 공)의 방향벡터이고
보라색 선이 외적 한 벡터를 의미한다
그리고 cVec(노란 공)은 외적한 벡터의 z 값을 나타내고 있다
이처럼 외적을 통해,
RotateVecTF 아래에 있을 때와 위에 있을 때를 확실히 구분할 수 있다
void Update()
{
CrossVector();
Vector3 dir = cVec - Vec3.position;
if (dir.magnitude >= 0.1f) Vec3.position += dir * Time.deltaTime * 5.0f;
Util.DrawLine(lineRenderer, RotateVecTF.right, Color.yellow, 10.0f);
}
void CrossVector()
{
Vector3 dir = Vec1.position - RotateVecTF.position;
cVec = Vector3.Cross(RotateVecTF.right, dir);
Util.DrawLine(lineRendererDir, dir, Color.magenta, 3.0f);
Util.DrawLine(lineRendererCross, cVec, Color.blue, 3.0f);
System.Text.StringBuilder sb = new System.Text.StringBuilder();
{
sb.Append("dir: " + dir);
sb.Append("\n");
sb.Append("cVec: " + cVec);
sb.Append("\n");
string str = cVec.z < 0 ? "아래에 위치" : " 위에 위치";// 굳이 내적하지 않고 cVec.z만 이용
sb.Append(str);
textMesh.text = sb.ToString();
}
}
특정 기준을 두고 상하 및 좌우 여부를 판단할 때,
특정 기준의 transform 만을 이용해 그 여부를 판단을 할 때는 문제가 발생한다
특히,
transform은 고정되어 있지만 회전을 해서 기울기가 생긴다면
단순히 transform을 통해 판단은 불가능하다
그래서 위 코드처럼 외적을 이용해서 판단을 한다
또한, RotateVecTF.right가 기준이 되어 dir을 외적 한 다음
굳이 Dot(내적)을 통해 스칼라 값으로 변경하지 않고 cVec.z값으로만 판단을 했다
정리
// 위에 나온 예시 코드들 중 일부
Vector3 dir = Player.position - Target.position;
Vector3 cross = Vector3.Cross(Player.forward, dir);
float dotUP = Vector3.Dot(cross.normalized, Vector3.up);
앞선 예시들을 통해 코드들을 분석하면
1) dir과 기준 오브젝트(ex. 플레이어)의 특정 방향을 외적을 하고
2) 그 외적한 벡터를 스칼라(값)로 변경하기 위해서
특정한 기준(ex. Vector3.forward)과 함께 내적 했다는 사실을 알 수 있다
다시 정리하면,
아래와 같은 형태로 작성이 된다
cross = Cross(dir, A)
dot = Dot(cross, B)
// dot의 부호를 통해 각도를 확인할 수 있다
그리고 A와 B에 들어오는 종류는 아래와 같다
A:
1) 기준 오브젝트(플레이어)의 forward:
주로 3D 백뷰 게임에서 사용된다
주로 캐릭터나 객체가 바라보는 방향을 나타낸다
2) 기준 오브젝트(플레이어)의 up:
주로 2D 탑뷰 게임에서 사용된다
주로 캐릭터나 객체의 상단 방향을 나타낸다
B:
A가 기준 오브젝트(플레이어) 의 Forward인 경우에,
1) Vector3.Up: 좌우 방향을 측정한다
2) Vector3.Right: 상하 방향을 측정한다
A가 기준 오브젝트(플레이어)의 Up인 경우에,
1) Vector3.Forward: 좌우 방향을 측정한다
2) Vector3.Right: 상하 방향을 측정한다
결국 핵심은
플레이어의 Up(2D) 혹은 Forward(3D) 벡터와 dir벡터의 외적 한 벡터를
우리가 원하는 기준 축과 내적 해서
그 값을 통해 각도 및 방향을 알아내는 것이다

'게임 수학 & 물리 > 게임 수학' 카테고리의 다른 글
| [게임 수학] 행렬(2) (0) | 2024.02.28 |
|---|---|
| [게임 수학] 행렬(1) (0) | 2024.02.27 |
| [게임 수학] 벡터의 외적 (1) (0) | 2024.02.25 |
| [게임 수학] 벡터의 내적 (2) (1) | 2023.10.28 |
| [게임 수학] 벡터의 내적 (1) (0) | 2023.10.28 |
