내적과 외적
벡터의 내적에서는 자신을 기준으로 앞, 뒤 방향을 확인할 수 있었다면
벡터의 외적에서는 자신을 기준으로 좌, 우 방향을 확인할 수 있다
또한, 벡터의 내적을 통해 각도를 알아냈다고 하더라도
어떤 방향(좌, 우)으로 각도를 틀어야 하는지 헷갈리는 경우가 생기기 때문에 이를 보완한다
물론, 외적의 결과값들은 내적을 통해서도 추론할 수 있지만
외적은 정규화 과정을 거치지 않아도 되기 때문에 연산에서 효율적이다
벡터의 외적

X와 Y를 외적해서 Z가 나온 그림이다
외적에서는 교환법칙이 성립되지 않는다는 점을 주의해야 한다
교환법칙이 성립되지 않는 외적에 대한 결과는 아래와 같다

왼손 좌표계 vs. 오른손 좌표계
손(왼손 or 오른손)을 이용해서 시작 벡터에서 가려는 벡터로 손을 감싸면
엄지손가락이 가리키는 방향이 외적 방향이다

언리얼, 유니티 둘 다 왼손 좌표계이고 표준 설정만 다를 뿐이다
벡터의 외적 공식
벡터의 내적의 결과는 값(스칼라)이 나왔지만
벡터의 외적의 결과는 벡터로 나온다
따라서, 외적의 결과를 이용하기 위해서
주로 외적의 결과벡터와 X, Y, Z 축 중 하나를 내적 하여 스칼라를 구해서 이용한다
1)

2)

2번째 공식은 ||을 통해 스칼라 값을 뽑아낸 것이다
결국은 sin 그래프에 따라 부호가 결정되고

위 sin 그래프를 통해 sin θ가 0인 0° 와 180° 에서 외적 값(스칼라)도 0이 된다는 것을 알 수 있다
따라서, 아래와 같은 형태의 외적 값이 나온다는 것을 알 수 있다

정리하면,
0°, 180° 일 때는 외적의 값이 0
0° ~ 180° 사이일 때는 양수
180° ~ 360° 사이일때는 음수가 나타나는 것을 알 수 있고
이를 통해 특정 기준을 두고 상하 방향 및 좌우 방향을 알 수 있다
또한, 평행인지 평행이 아닌지도 확인이 가능하다
외적과 평행사변형의 상관관계
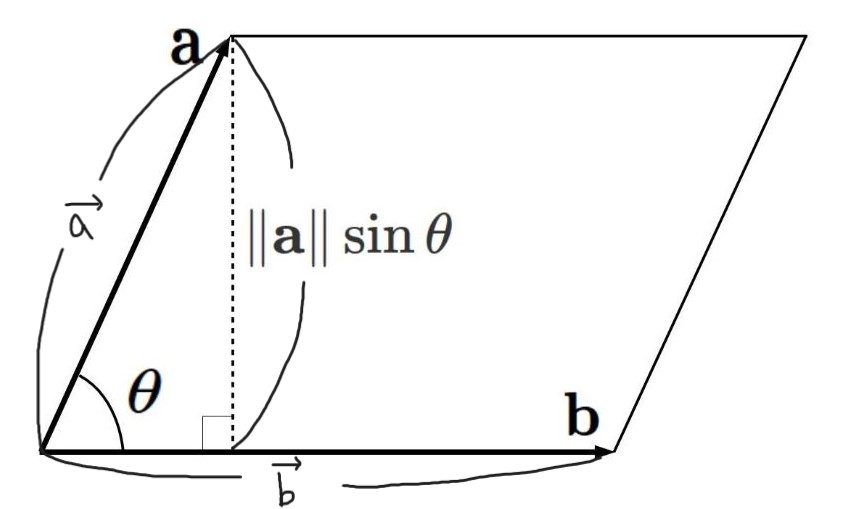
위 그림을 통해 평행사변형의 넓이는
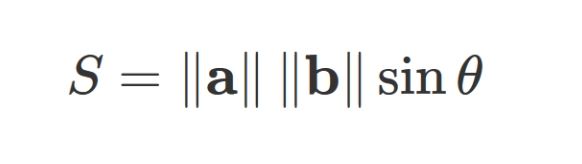
라는 사실을 알 수 있다
이는 a와 b의 외적 한 스칼라 값인
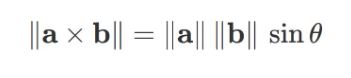
와 같기 때문에
결국, 외적한 값과 평행사변형의 넓이는 동일하다는 사실을 알 수 있다
'게임 수학 & 물리 > 게임 수학' 카테고리의 다른 글
| [게임 수학] 행렬(1) (0) | 2024.02.27 |
|---|---|
| [게임 수학] 벡터의 외적(2) (0) | 2024.02.26 |
| [게임 수학] 벡터의 내적 (2) (1) | 2023.10.28 |
| [게임 수학] 벡터의 내적 (1) (0) | 2023.10.28 |
| [게임 수학] 벡터의 기초 (2) (0) | 2023.10.17 |
