# 백트래킹 개념
그래프를 완전(모두) 탐색하는 것이 아니라
찾는 답일 가능성이 있는 경우에만 탐색하고
찾는 답일 가능성이 없는 경우에는 재귀를 통해
가장 최근에 방문했던 노드로 돌아가는 것이 핵심이다
# 백트래킹 과정
쉬운 백트래킹 알고리즘은 그냥 풀어도 되지만
난이도가 있을수록 아래의 단계를 거쳐 확실하게 구현해야 한다
1) 상태 정의: 문제의 각 단계를 그래프의 상태로 정의
2) 유망함수(IsPromising): 현재 상태가 유망한 지 여부를 확인
3) 해결책 확인(IsSolution): 현재 상태가 문제의 답인지 여부를 확인
4) 재귀 호출: DFS처럼 재귀를 이용해 유망한 상태로 이동
// 백트래킹을 하기위해서는 반드시 상태 정의를 해야한다
// 유망성 판단 함수
bool isPromising(int level, State state) {
// 현재 상태가 유망한지 판단하는 로직을 구현합니다.
}
// 해결책 확인 함수
bool isSolution(State state) {
// 현재 상태가 문제의 해결책인지 판단하는 로직을 구현합니다.
}
// 백트래킹 함수
void backtrack(int level, State state) {
// 현재 상태가 해결책이면 처리
if (isSolution(state)) {
processSolution(state);
return;
}
// 다음 가능한 상태를 탐색
for (State nextState : possibleStates(state)) {
if (isPromising(level, nextState)) {
backtrack(level + 1, nextState);
}
}
}..
# 예시 문제 1 - 부분 합
문제)
{1, 2, 3, 4}로 이루어진 집합에서 숫자를 뽑아서 합이 5인 조합 구하기
완전탐색 방법)

완전탐색을 하면 O(2^N)로 모든 경우의 수를 다 확인해야 한다
백트래킹 방법)

1. 상태 정의: 현재까지 선택한 숫자들의 합
2. IsPromising: 현재 부분 합이 목표 값을 초과하면, 유망하지 않다고 판단
3. IsSolution: 현재 부분 합이 목표 값과 일치하는지 확인
4. 재귀: 다음 숫자를 선택하여 부분합 갱신
참고로 해(정답)가 여러개인 경우에는
한 번만 return을 해서 계속 해를 찾도록 해야 한다
#include <iostream>
#include <vector>
using namespace std;
// 사용할 숫자들
vector<int> nums = {1, 2, 3, 4};
// 목표 합
int target = 5;
// 현재 조합
vector<int> current;
void findCombinations(int index) {
int sum = 0;
for (int num : current) {
sum += num;
}
// 조건 1: 현재 조합으로 합이 target이 되면 결과를 출력하고 더 탐색하지 않음
if (sum == target) {
for (int num : current) {
cout << num << " ";
}
cout << endl;
return;
}
// 조건 2: 합이 target을 초과하면 더 탐색하지 않음
if (sum > target) {
return;
}
// 유망한 경우에만 다음 숫자를 추가하여 탐색을 계속함
for (int i = index; i < nums.size(); ++i) {
current.push_back(nums[i]);
findCombinations(i + 1);
current.pop_back(); // 현재 숫자를 조합에서 제외하여 다음 경우를 탐색
}
}
int main() {
findCombinations(0);
return 0;
}
# 예시 문제 2 - N 퀸
문제)
N * N 체스판에서 체스의 퀸을 N개 배치했을 때
서로 공격할 수 없는 위치에 놓을 수 있는 방법의 경우의 수 확인
(퀸은 현재 자신위치 기준 8방향 직선방향으로 공격 가능)

완전탐색 방법)
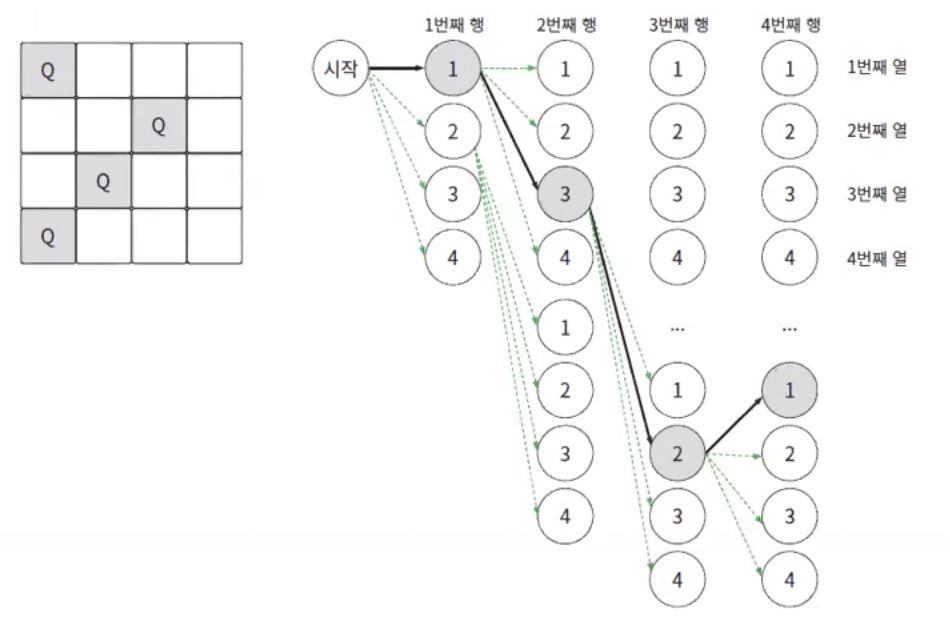
백트래킹 방법)
1. 상태 정의: 각 행에 하나의 퀸이 위치하도록 함
2. 유망 함수: 현재 행에 퀸을 놓았을 때, 다른 퀸과 충돌하는지 확인
3. 해결책 확인: 모든 퀸이 배치되었는지 확인
4. 재귀 호출: 다음행에 퀸을 배치
유망 함수를 쉽게 작성하기 어려운 경우에는
아래와 같이 아이디어를 정리하고 그에 맞는 유망 함수를 작성하면 된다
유망 함수 아이디어 1: 각 행의 동일한 열에 퀸이 배치되지 않도록 함
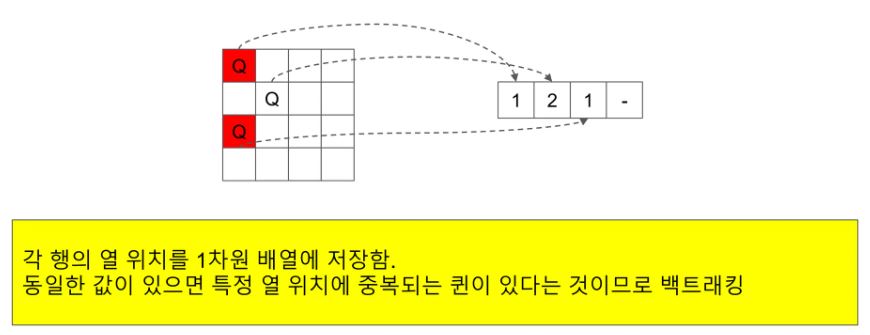
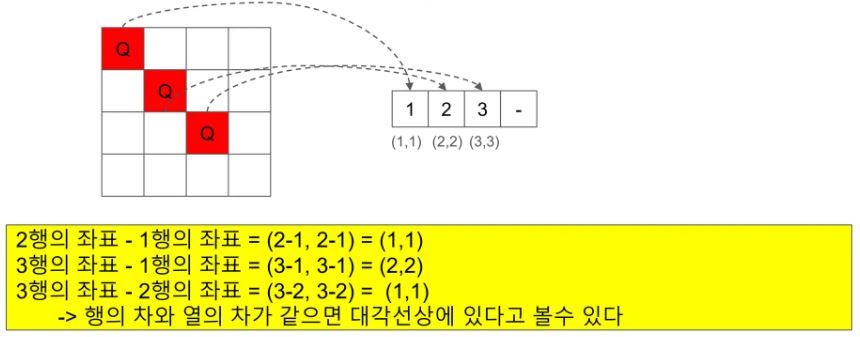
유망 함수 아이디어 2: 각 행의 퀸들이 대각선 방향(오른쪽 아래, 왼쪽 아래)에 겹치지 않도록 함
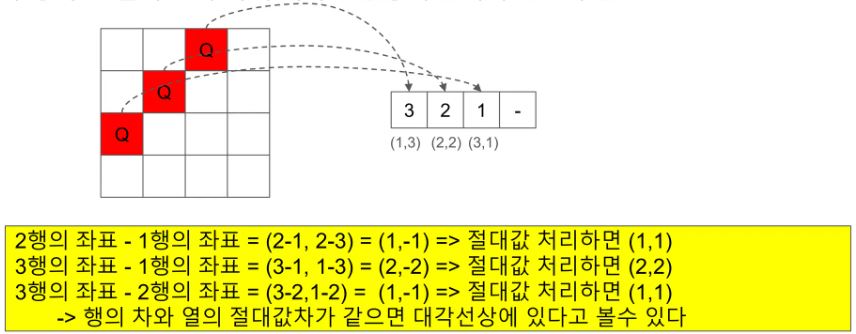
유망 함수 아이디어 결론:
1번 아이디어인
각 행의 동일한 열에 퀸이 배치되지 않도록 하기 위해
각 열의 값이 같은지 확인을 하면 된다
2번 아이디어인
각 행의 대각선에 같은 퀸이 배치되지 않도록 하기 위해
오른쪽 방향은 행과 열의 차가 같은지 확인,
왼쪽 방향은 행과 열의 절대값 차가 같은지 확인을 하면 된다
그런데 왼쪽 방향만 커버하면 오른쪽 방향은 커버가 되기에
행과 열의 절대값 차가 같은지를 확인하는 왼쪽 방향만 확인하면 된다
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
// N Queen 문제: n x n 체스판에 n개의 퀸을 서로 공격하지 못하게 배치하는 문제
const int N = 4; // 퀸의 개수
vector<int> board(N, -1); // 보드 배열, 인덱스는 행을, 값은 열을 나타냄
// 보드의 현재 상태를 출력하는 함수
void printBoard() {
// 각 행을 반복
for (int i = 0; i < N; ++i) {
// 각 열을 반복
for (int j = 0; j < N; ++j) {
// 현재 위치에 퀸이 있는지 확인
if (board[i] == j) {
cout << "Q "; // 퀸이 있으면 "Q" 출력
} else {
cout << ". "; // 퀸이 없으면 "." 출력
}
}
cout << endl; // 한 행이 끝나면 줄바꿈
}
cout << endl; // 보드 전체 출력 후 줄바꿈
}
// 현재 위치에 퀸을 놓아도 되는지 확인하는 유망함수
bool isSafe(int row, int col) {
// 현재 행 이전의 모든 행을 검사
for (int i = 0; i < row; ++i) {
// 1. 같은 열에 퀸이 있는지 확인
if (board[i] == col) {
return false; // 같은 열에 퀸이 있으면 false 반환
}
// 2. 같은 대각선에 퀸이 있는지 확인
if (abs(board[i] - col) == abs(i - row)) {
return false; // 같은 대각선에 퀸이 있으면 false 반환
}
}
return true; // 어떤 충돌도 없으면 true 반환
}
// N Queen 문제를 해결하기 위한 재귀 함수
void solveNQueens(int row, int &solutions) {
// 모든 행에 퀸을 배치한 경우 (기저 조건)
if (row == N) {
// 해결책을 찾았으므로 해결책 수 증가
solutions++;
// 현재 보드 상태를 출력
printBoard();
return; // 함수 종료
}
// 현재 행의 모든 열에 대해 반복
for (int col = 0; col < N; ++col) {
// 현재 위치에 퀸을 놓을 수 있는지 확인
if (isSafe(row, col)) {
board[row] = col; // 현재 행의 열에 퀸을 놓음
solveNQueens(row + 1, solutions); // 다음 행에 대해 재귀 호출
// 퀸을 제거할 필요 없음, 다음 반복에서 덮어쓰기 때문에
}
}
}
int main() {
int solutions = 0; // 해결책 수를 저장할 변수
solveNQueens(0, solutions); // 첫 번째 행부터 시작
cout << "총 해결책 수: " << solutions << endl; // 총 해결책 수 출력
return 0;
}'자료구조 & 알고리즘 > [합격자되기] C++ 코딩테스트' 카테고리의 다른 글
| [코테 합격자 되기] 15장 동적계획법 (0) | 2024.12.17 |
|---|---|
| [코테 합격자 되기] 13장 정렬 (0) | 2024.12.16 |
| [코테 합격자 되기] 11장 그래프 (0) | 2024.12.14 |
| [코테 합격자 되기] 10장 집합 (0) | 2024.12.13 |
| [코테 합격자 되기] 09장 트리 (0) | 2024.12.13 |
