sin, cos
게임에서 sin, cos은
특정 패턴의 움직임을 구현할 때
sin, cos을 활용할 수 있다
sin, cos, tan의 공식
sin, cos, tan의 공식은 아래와 같다

sin, cos의 활용

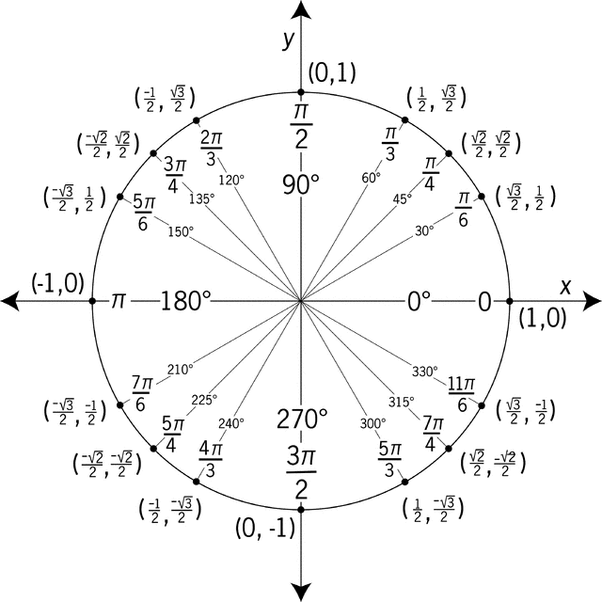
단위원(반지름이 1인 경우)을 기준으로 했을 때
각도( θ )를 알면 원에서의 해당 좌표를 알 수 있는 것이 핵심이다
위 그림처럼 cos θ , sin θ가 우리가 원하는 x, y 좌표를 의미한다
이처럼
cos θ 는 x좌표가 1부터 시작하고
sin θ 는 y좌표가 0부터 시작하며
각각 sin cos tan는 아래와 같은 그래프를 그리는 것을 알 수 있다
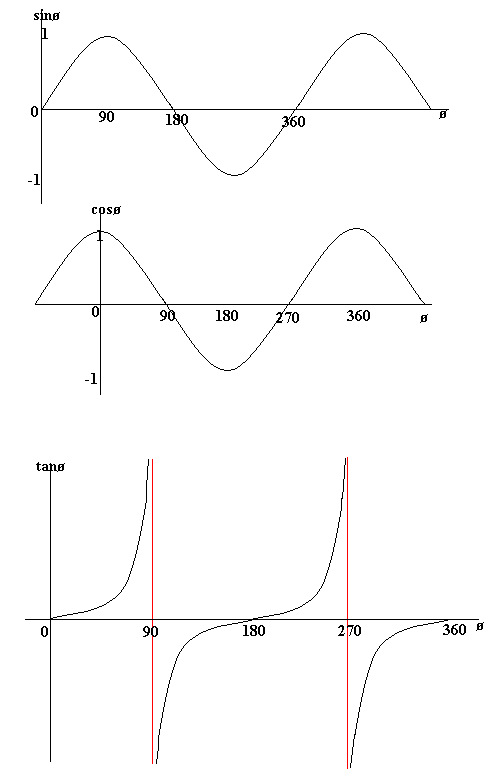
이렇게 sin, cos을 통해서
각도로 원에서의 위치를 알아낼 수 있었다
또한, sin, cos의 그래프에서 반복적인 형태로 위아래로 움직이는 점을 활용해서
게임에서 다양한 패턴을 구현할 수 있다
라디언(Radian)
일상생활에서는 θ(세타)인 ° 단위를 이용하여
각도를 표현하지만
수학에서 원의 길이는 Radian(호도법)을 이용한다
따라서 라디언에 대해 간단하게 알아보면
반지름의 길이와 호의 길이가 같을 때를 1 Radian이라고 한다

그리고 180° 기준으로 위 그림처럼 3 Radian + 0.14.. 가
결국 180° 를 의미하며 π(파이)를 뜻한다
다시 정리하면,
180° = 3.14 라디언 = π(파이)
360° = 2 π
가 되는 것이다
그리고
1 라디언의 각도는 180/π 로 대략 57.32°
1° 를 라디언으로 변환하면, π/180
30° 를 라디언으로 변환하면, 30 * π/180 = 대략 0.52 Radian
이처럼 변환이 가능하다
각도를 넣으면 라디언으로 바꿔주는 기능은 당연히 유니티에도 있으며
Mathf.Deg2Rad, Mathf.Rad2Deg를 통해 상호 간 변환이 가능하다
이렇게 배운 것들을 활용하면
아래와 같은 그림은 쉽게 이해가 가능해진다
'게임 수학 & 물리 > 게임 수학' 카테고리의 다른 글
| [게임 수학] 벡터의 기초 (2) (0) | 2023.10.17 |
|---|---|
| [게임 수학] 벡터의 기초 (1) (0) | 2023.10.17 |
| [게임 수학] tangent (0) | 2023.10.16 |
| [게임 수학] sin, cos (2) (0) | 2023.10.16 |
| [게임 수학] 피타고라스의 정리 (0) | 2023.10.15 |
